Simple Machines

Usually the term refers to the six classical simple machines which were defined by Renaissance scientists:^[4]

• Lever
• Wheel and axle
• Pulley
• Inclined plane
• Wedge
• Screw

They are the elementary "building blocks" of which all complicated machines are composed.^[3][5]For example, wheels, levers, and pulleys are all used in the mechanism of a bicycle.

In themselves, three are composites of the other three.  The basic machines are the inclined plane, the lever, and the wheel.  The composite machines are the pulley (wheel & lever), the wedge (lever and plane), and screw (wheel and plane).

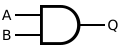
That said, in computers, the same basic breakdown happens (at least on the human level).  We have the building blocks of logic: AND (true if both are true), NOT (true if false), and OR (true if one is true), and the composite logical elements: XOR (true if one or the other, but not both, are true) and XNOR (true if one or the other, but not both, are false), however, it turns out that on the chip level, what would seem to be the final 'composites' NAND (true if "both are true" is false) *or* NOR (true if "either are true" is false) are the *actual* building blocks of logic chips.

Here's logic building with 'NAND':

NAND

This is a NAND gate; trivially, just a NAND gate is used to realise it:

Desired Gate	NAND Construction
Truth Table Input A Input B Output Q 0 0 1 0 1 1 1 0 1 1 1 0

[edit]NOT

A NOT gate is made by joining the inputs of a NAND gate. Since a NAND gate is equivalent to an AND gate followed by a NOT gate, joining the inputs of a NAND gate leaves only the NOT part.

Desired Gate	NAND Construction
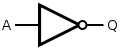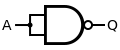Truth Table Input A Output Q 0 1 1 0

[edit]AND

An AND gate is made by following a NAND gate by a NOT gate as shown below. This gives a NOT NAND, i.e. AND.

Desired Gate	NAND Construction
Truth Table Input A Input B Output Q 0 0 0 0 1 0 1 0 0 1 1 1

[edit]OR

If the truth table for a NAND gate is examined, it can be seen that if any of the inputs are 0, then the output will be 1. However to be an OR gate, if any input is 1, the output must also be 1. Therefore, if the inputs are inverted, any high input will trigger a high output.

Desired Gate	NAND Construction
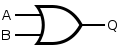Truth Table Input A Input B Output Q 0 0 0 0 1 1 1 0 1 1 1 1

[edit]NOR

A NOR gate is simply an OR gate with an inverted output:

Desired Gate	NAND Construction
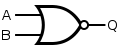Truth Table Input A Input B Output Q 0 0 1 0 1 0 1 0 0 1 1 0

[edit]XOR

An XOR gate is constructed similarly to an OR gate, except with an additional NAND gate inserted such that if both inputs are high, the inputs to the final NAND gate will also be high, and the output will be low. This effectively represents the formula (A OR B) AND (A NAND B).

Desired Gate	NAND Construction
Truth Table Input A Input B Output Q 0 0 0 0 1 1 1 0 1 1 1 0

[edit]XNOR

An XNOR gate is simply an XOR gate with an inverted output:

Desired Gate	NAND Construction
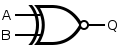Truth Table Input A Input B Output Q 0 0 1 0 1 0 1 0 0 1 1 1